| MATHEMATICS | |
| Aliquot and Factor Trees Diagram linking numbers by the sum of their factors, bottom diagram includes 1, bottom top does not. | 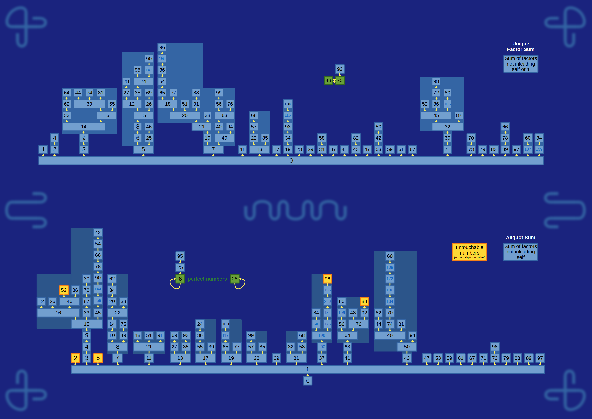 |
| Cistercian Numbers Invented by medieval monastery | 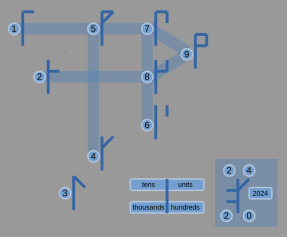 |
| Collatz Conjecture (working up from 1, numbers below 1000) | 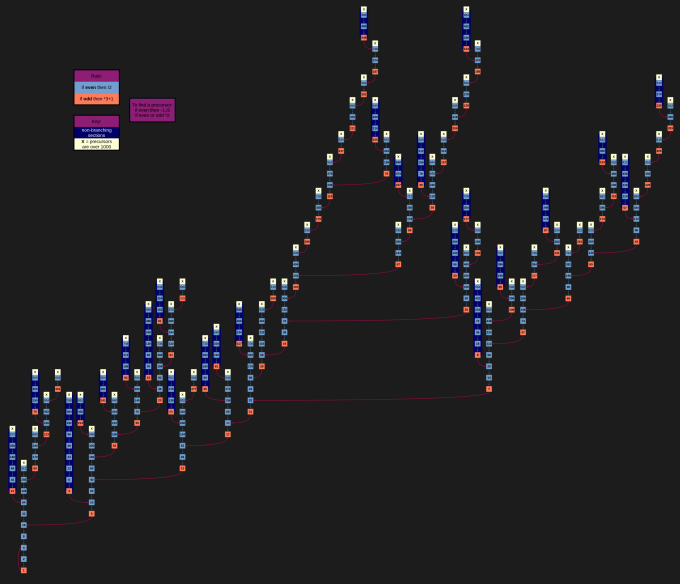 |
| A chart of numbers and the most square rectangle they can be. Primes end up very tall, square numbers are actually square. Below is a later version continued up to 100 | 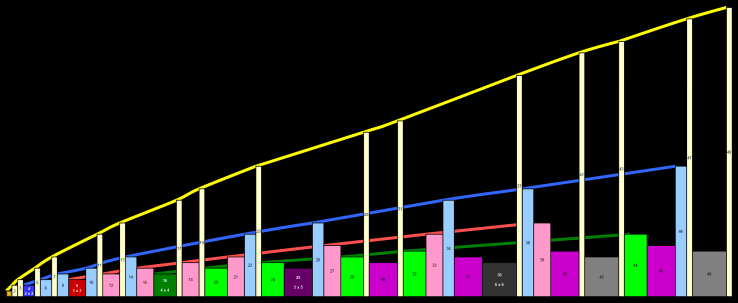 |
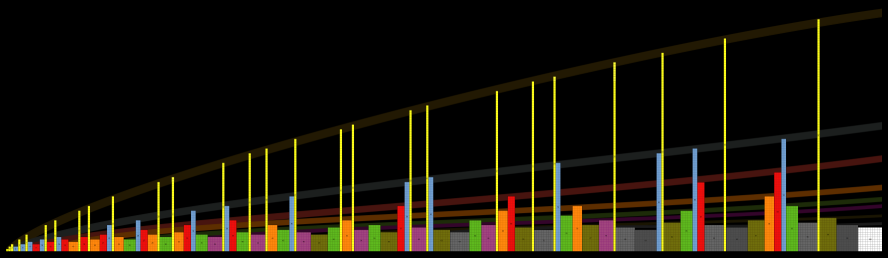 | |
| A chart of numbers sorted by the complexity of their factors. It shows numbers from 1 to 151. The primary numbers are in yellow and the rest of the numbers (except 1) are composite numbers of increasing levels of compelxity up the diagram. | 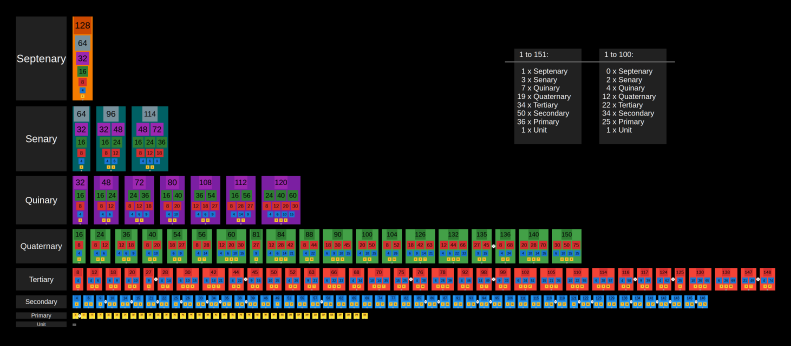 |
| A diagram depicting trees of numbers connecing to their digit sum. This is what you get when you add up all the digits of a number, so for 12, you would do the sum 1+2=3 The numbers 1 to 300 are used to create the chart. |  |
| A diagram of numbers and their divisors. Yellow is prime numbers, blue is highly composite numbers. Coloured products of division are all whole numbers. The black line joins square numbers. | 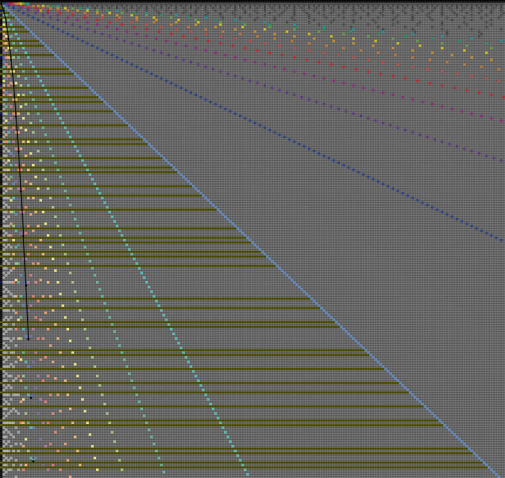 |
| Ecstatic Numbers Cube Happy numbers, calculated by summing the cube of each digit. So 12 becomes 1³ + 2³ = 9 |  |
| Four Fours Solutions to the first sixty numbers The key shows an explanation to the units used and how they are made to fours. The idea here is to make as many numbers as possible using four "4" and as many operands as needed. Note that power numbers count. |  |
| Grandi's Series A series equal to 1 - 1 + 1 - 1 ... which is a non-convergent series. Using brackets we can make it sum to 0, 1 or -infinity. Using better methods we get the result 1/2, which is the commonly accepted result. |  |
| Happy & Sad Numbers A Happy number is one that reaches 1 when you add up the square of the digits, and repeat. Sad numbers end up in a cycle including 4. Uses numbers 1 to 100. |  |
| Letters and the first Numbers they can be found in. |  |
| First ~100 numbers in Modulus 6, showing patterns of primes and polygonal numbers | 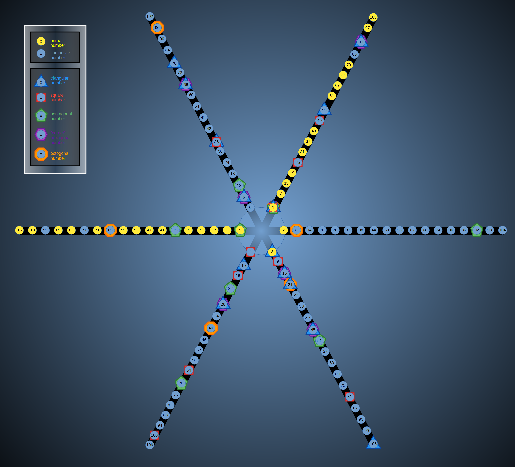 |
| First ~100 numbers in Mod 10, showing patterns of primes and polygonal numbers |  |
| First ~100 numbers in Mod 12, showing patterns of primes and polygonal numbers |  |
| Number types as a Euler diagram If you have details or fixes for this, please let me know | 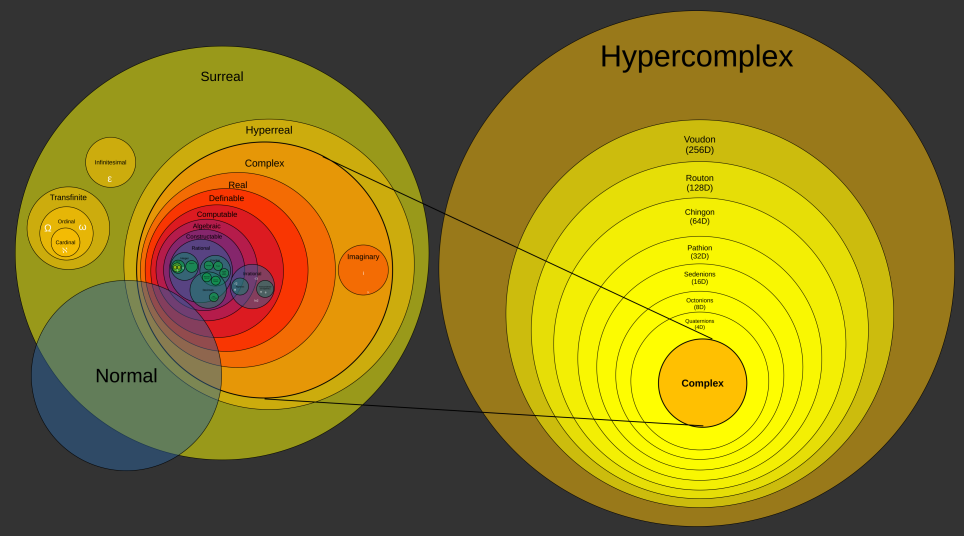 |
| Origami bases relationships | 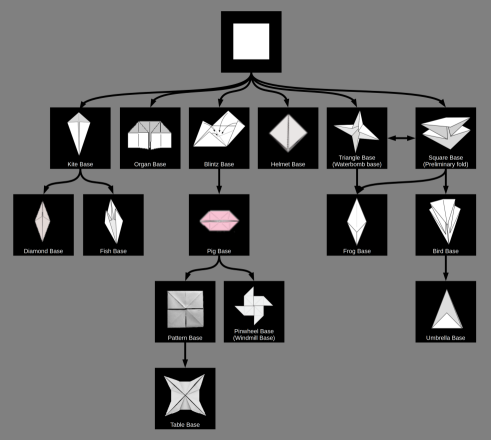 |
| Polygon types tree If you know of more terms for pentagons, please let me know | 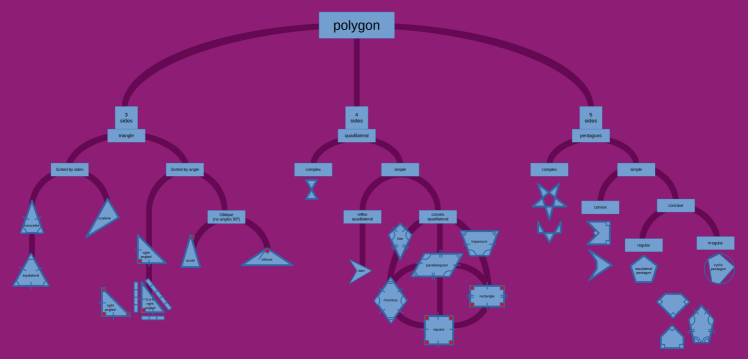 |
| Polyhedra types A diagram of all regular, semi-regular and select other solids. |  |
| Polyhedra regular apex types. | 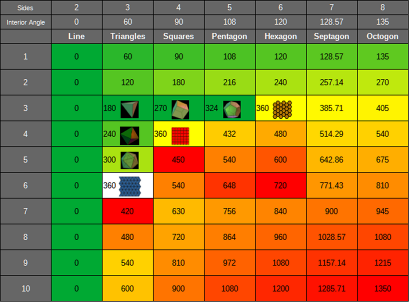 |
| Polyhedra semi-regular apex types. | 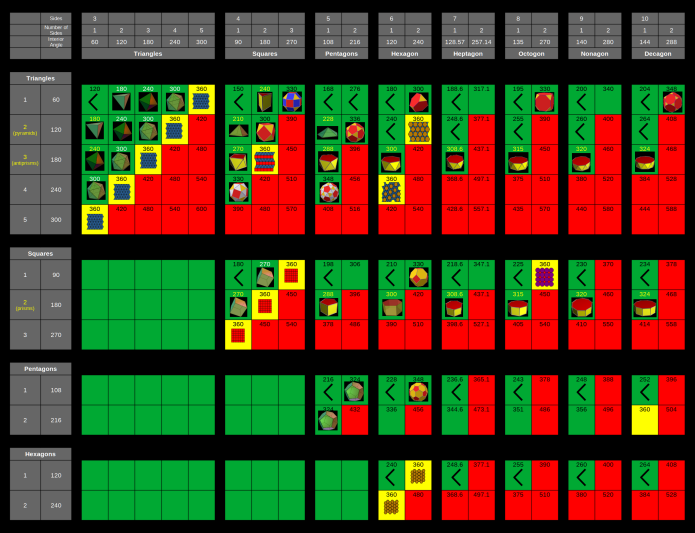 |
| Primary, Secondary, Tertiary Numbers Numbers from 1 to 100 classified by the compelxity of their factors. Primary (prime) numbers only have 1 and themselves as factor. Secondary numbers have one or two primes as factors. Tertiary numbers have at least one secondary number as factors. | 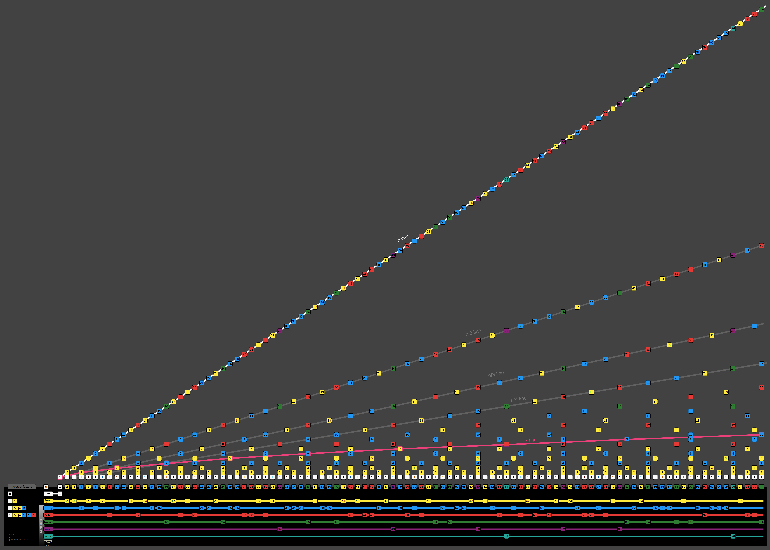 |
| Prime Factors as Houses Each number broken down into it's composite factors, taller houses having more factors and prime numbers being one-storey |  |
| Prime Glitching This process takes the prime factors of each number, and adds them to their exponent then multiplies them together. There's an example in the top rtight of the diagram. Thanks to Combo Class for exploring them in this video. | 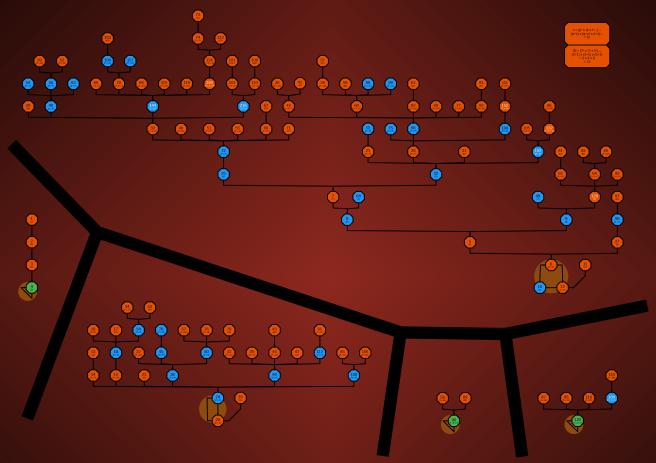 |
| Prime numbers and their relationship to the square root line. This demonstrates why some name numbers below 4 as "sub prime" as there are literally no numbers between 1 and their root to be a factor. Under this view, 5 would be the first proper prime number. | 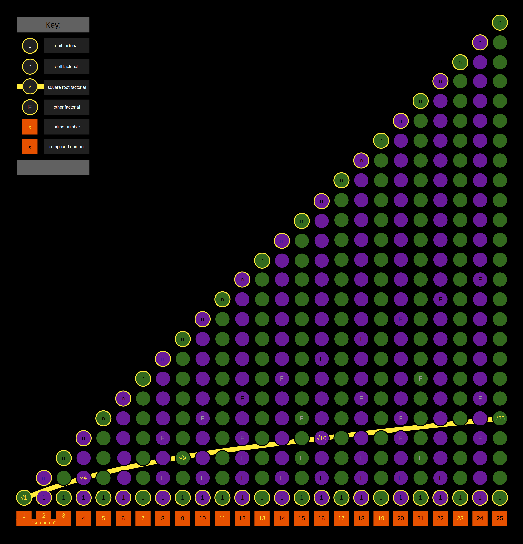 |
| Set Theory A diagram showing how numbers can be built. Starts with the empty set, representing zero, 1 is made by creating a set of that set. |  |
| Sieve of Eratosthenes A way of finding Prime numbers by removing the multiples of numbers starting with 2. |  |
| Sprouts maths game diagram. Each player takes a turn joining two dots and with a line and putting a new dot on that line. Dots can only have up to 3 lines linked to them. | 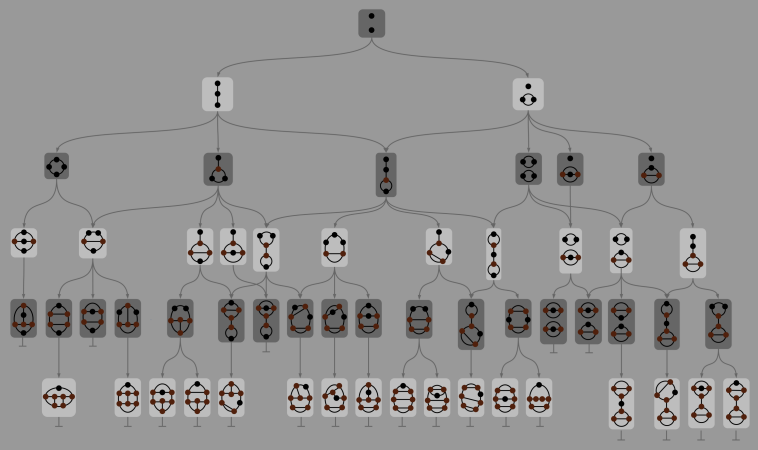 |
| A chart of Stellar Polygons with 12 or fewer corners | 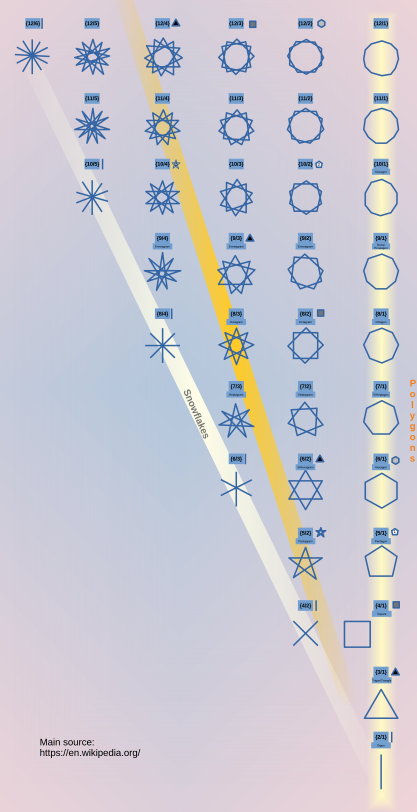  |
| Wheel Factors up to 30, howing distribution of primes and composite numbers | 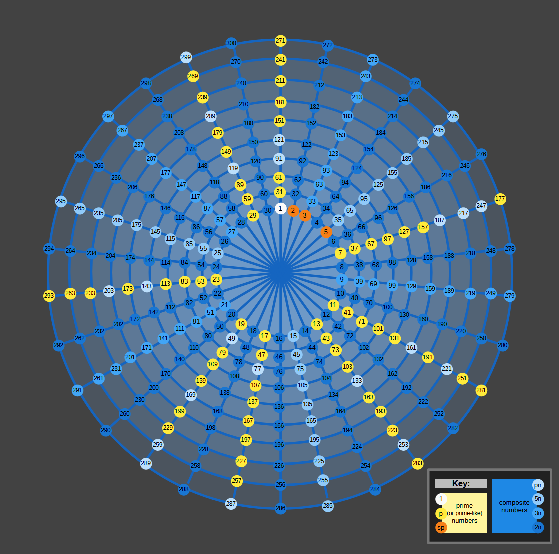 |
| A chart of numbers and their word length | 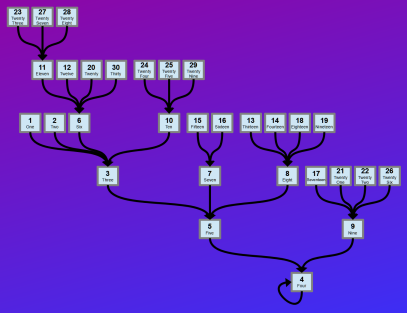 |
| A similar chart showing all numbers up to 100 and a few otheras. | 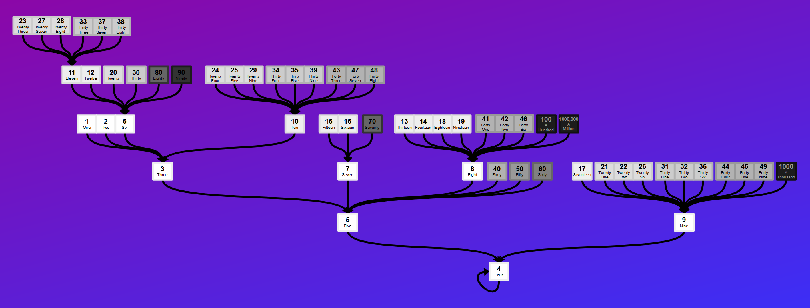 |